Comparative Analysis of Three Lebanese Textbooks Based on the Topic of Parallelogram

 

Comparative Analysis of Three Lebanese Textbooks Based on the Topic of

Parallelogram

تحليل مقارن لثلاثة كتب مدرسية لبنانية على أساس موضوع متوازي الأضلاع

 

/ إيلي الخوريMr. Elie Khoury^{)[1] (}

/ روز صفيرMrs. Rose Sfeir^{)[2] (}

/ أ.د. نعيم الرويديProf. Naim   El Rouadi^([3]) 

تاريخ الاستلام:21-1-2023       تاريخ القبول: 27-1-2023       تاريخ النشر 31-3-2023

ملخص

إستنادًا إلى موضوع متوازي الأضلاع المتضمّن في منهج الرّياضيّات للصف الثّامن في لبنان، تقدّم هذه الدّراسة تحليلًا مقارنًا للمهام الموجودة في ثلاث كتب مدرسية لبنانية. وفقا للدراسات، يمكن أن يكون لاستخدام الكتب المدرسية تأثير على أداء الطلاب في الرياضيات، لا سيما في هندسة  أقليدس. من المهم أن توفر الكتب المدرسية توازنًا بين مجموعة من المهام لأنّ طبيعة المهام قد تؤثر على طريقة تفكير التلاميذ. بالإضافة إلى ذلك، لم تكن هناك مقارنة في مجال  هندسة أقليدس في الكتب اللبنانية المدرسية  حتى الآن. تستعمل هذه الدراسة إطار عمل Glacin (2018)  خماسي الأبعاد لتحقيق هدف تحليل مهام الكتاب المدرسي. يركز التحليل على المحتوى الرياضي والنّشاط الرّياضي، ومستوى التعقيد، وشكل الإجابة، وسياق المهام ويشمل 742 مهمّة. تشير النتائج إلى أن الكتب المدرسية لا توفر مجموعة متنوعة من المهام. ينصب التركيز على الأشكال الهندسية، والحدل والإستدلال، وأجراء الروابط، والأسئلة المفتوحة والمهام الغير تطبيقية في جميع الكتب المدرسية.

الكلمات المفاتيح: كتب الرياضيات، متوازي الأضلاع، تحليل المهام، المنهج، تحليل المحتوى.

1.Abstract :

This study presents a comparative analysis of tasks observed in three Lebanese textbooks based on the topic of parallelogram. According to different studies, the use of textbooks can have an impact on students’ mathematics performance, particularly in Euclidean geometry. It is crucial that textbooks offer a balance between a range of tasks because their nature may affect how students think. Additionally, there hasn’t been any comparison of the geometry content in textbooks in Lebanon yet. This study used Glacin’s (2018) 5-dimensional framework to achieve the goal of analyzing textbook tasks. The analysis focuses on mathematical content, mathematical activity, complexity level, answer form, and context of tasks and encompasses 742 tasks. The findings indicate that the three textbooks don’t present a wide variety of tasks. The focus is on geometric shapes and solids as content, argumentation and reasoning as activities, making connections as a complexity level, open-ended questions as answer forms, and non-application tasks as context in all textbooks.

Keywords:

Mathematics textbooks, parallelogram, tasks analysis, mathematics curriculum, mathematical content analysis.

1. Rationale and significance of the study

As Mithans&IvanusGremek (2020) mentioned in their article, multiple educational resources are used within the classroom. Among these resources, textbooks are possibly the major source that is utilized as a reference for teachers and students.Abdullah & Shin (2019) defined textbooks as books created and produced to convey the national curriculum and the required education goals. According to the authors, textbooks are a crucial part of the education system and curriculum, so much so that they have become synonymous to learning and teaching process in schools.

Remillard, (2000) believes that the choice of the textbook is a good indication of a curriculum, and an examination of textbooks gives us an important look into how effectively the desired curriculum is implemented.According to Valverde et al. (2002), the organization of mathematics’ textbooks may have an influence on how students are taught in the classroom. The authors claim that different pedagogical approaches used in mathematics classrooms are impacted by the design and organization of textbooks, even if those textbooks are based on the same national curriculumsuch as, in our case, Lebanon.

Valverde et al., (2002) also mentioned that textbooks are considered to be the most important component of a curriculum, mainly because they serve as a mirror of the curriculum for parents, teachers and students. Rezat (2013), asserts that for teachers, textbooks serve as a source of curriculum material, a paradigmatic presentation of a body of structured information, and a recommendation of instructional approaches. For students, they serve as a reliable source of information and a crucial tool for enhancing subject-matter understanding through their recommended tasks. As a result, every textbook presents a distinct perspective on mathematics.

As per Johansson (2007), textbooks are utilized in mathematics classes all over the world on a regular basis. The author claims that before till today, people did not recognize the value of textbooks as much. To stress that textbooks both represent the national curriculum and have a significant impact on teaching methods, a level called “possibly implemented curriculum” was added between intended curriculum and implemented curriculum.

Many researches have demonstrated the link between textbooks and students learning. For instance, according to Valverde et al. (2002), the Third International Mathematics and Science Study (TIMSS) has unmistakably shown that, across nations, the handling of linked themes in the curriculum and textbooks has a strong correlation with students’ learning. Xin (2007)looked into how different learning possibilities in a Chinese and an American mathematics textbook can affect students’ ability to solve problems.According to the study, there is a link connecting students’ ability to solve mathematical problems and how those problems are presented in textbooks.

Usiskin (2013) also discussed the American experience, where classroom activities are more focused on what is printed in textbooks than on what the intended curriculum is. These results support Howson’s (1995)old hypothesis that textbooks reflect classroom reality more accurately than curriculum outlines. As a result, the findings of the textbook study could present a more comprehensive and in-depth view of both curriculum requirements and instructional strategies.

Fan et al. (2018), note that the textbooks are now the focus of worldwide study. This underlines the importance of textbooks in both teaching and learning mathematics. In Lebanon, textbooks are typically bought by parents or local groups, guaranteeing that each student has a copy of the books that the school has selected. The textbooks are used to do homework at home and are taken to each math lesson.

The rationale of this article is that the math textbook represents an essential element of school tools for the community: students, parents, teacher and pedagogical supervisor. For this reason, the comparison of textbooks will be a necessity for the choice of a textbook coherent with the curriculum. This study on the parallelogram is part of this comparison.

2. Literature review:

It seems to us that there is currently no study in the literature that compares Lebanese 8th grade mathematics textbooks. There are, however, several similar studies for other countries, with some research focusing on geometry and quadrilaterals.

In order to comprehend better the discrepancies between Malaysian and South Korean students’ success levels as discovered in the Trends in International Mathematics and Science Study (TIMSS), a study was conducted by Abdullah & Shin (2019) that compares quadrilaterals topic content in mathematics textbooks between Malaysia and South Korea. According to the data found, there are four key differences between how quadrilaterals are taught in the two nations. These factors include how the quadrilateral subjects are organized; how deeply exploration activities are explored; how deductive reasoning is incorporated into the learning content, and how challenging the problems at the chapters’ end are. In this regard, the authors advise that the Malaysian Ministry of Education’s Division of Curriculum Development evaluate the geometry content of the current mathematics textbook to conform to the curricula that has been shown to create students who do well on international examinations.

Usiskin et al. (2008) used a number of American textbooks to perform a micro curricular study on the topic of quadrilaterals. It addressed the question of whether a certain quadrilateral may have an identical mathematical definition that is either inclusive or exclusive. In addition, the examination was based on the geometric thinking level in the Van-Hiele model.

Another study was conducted by Hong & Mi Choi (2018) that evaluated and compared reasoning and proving opportunities in geometry lessons from American standard-based textbooks and Korean textbooks to better understand how these textbooks give students the opportunity to engage in reasoning and proving tasks. This study compared the exercises based on the Statement Type, Expected Activity, and Justification Type.  Overall, over 40% of Core Plus Mathematics Project (CPMP) exercise questions require reasoning and proving tasks, whereas 20% of Korean textbook exercise problems require reasoning and proving activities. One of the most important discoveries is that Koren and CPMP students have distinct options for geometry learning. According to the authors, it could be interesting to look at the geometric reasoning and proving abilities of Korean and CPMP students to determine how textbooks affect their learning.

Otten, Males & Gilbertson (2013) examined the reasoning, and proving opportunities in six US geometry textbooks, paying special emphasis to the topic of proof. The study focused on the sorts of reasoning and proving tasks demanded of students, as well as the type of mathematical statement around which the reasoning and proving occurred, whether general or specific. The results showed that reasoning-and-proving chances in student activities were mostly of the specific kind, whereas textbook exposition was mostly of the broad type. Opportunities for students to generate proofs were less prevalent in the chapters introducing proof than problems involving conjectures and assertions or exercises regarding the reasoning-and-proving process. Opportunities to reflect on the reasoning-and-proving process were plentiful in the introduction chapters, but scarce in the rest of the volumes.

Hidayah&Forgasz (2020) looked at the types of mathematical geometry tasks in two Australian and two Indonesian seventh-grade mathematics textbooks. The quantitative data were gathered from the coding outcomes of the textbooks’ tasks. The tasks were divided into six categories: Presentation forms, cognitive requirements, contextual aspects, information presented; numbers of steps required in the solution,and number of answers. The similarities and contrasts between the mathematical tasks presented in the chosen textbooks were examined. According to the coding results, the bulk of tasks in both the Australian and Indonesian textbooks were provided verbally and in combination. The four textbooks still emphasized routine and closed tasks. More than 93% of the problems in the four textbooks provided students with enough knowledge to solve the problem. The proportion of tasks with real-world context was greater in the Australian textbooks than in the others.

Fan, Mailizar, Alafaleq, Wang (2018) conducted a comparative research aimed at examining how geometric proof is addressed in secondary school mathematics textbooks in China, Indonesia, and Saudi Arabia, as well as exploring the similarities and contrasts shown in the textbooks of these three countries. The findings demonstrate that, while all of the textbooks from these nations covered geometric proof subjects, they differed significantly in three areas: The number of examples, the distribution of contents and, to a lesser extent, the types of proof.  China’s textbooks include the biggest proportion of geometric content and devote the most emphasis to the topic of proof itself. The national mathematics curriculum has certainly a major role in the observed discrepancies.

Other materials are used in classrooms, although not nearly as extensively as textbooks, claims (Glacin, 2018). The outcomes also demonstrated that the quality of textbook tasks was the most crucial consideration for teachers when selecting a textbook. The author asserts that mathematics textbooks are essential to mathematics education and students extensively employ textbook tasks for practices. It is important that textbooks offer a balance of variety of tasks because the tasks’ type may affect how students think.

We are especially interested in how selected Lebanese grade 8 textbooks present the concept of quadrilaterals, in the tasks they give to help students consolidate and systematize their information, and in discovering additional similarities and variations amongst textbooks. The type of the tasks provided to students is the primary focus of this study.

3. Cognitive impact of the textbook

The current study places a strong emphasis on mathematical tasks. According to Christiansen &Wealther (1986), tasks are defined as suggestions and challenges provided by the teacher or textbook or students himself (In some cases) that comprise a goal to achieve.

According to Skovsmose (2001), the teacher “encourages” the student to participate in the task. The student’s reaction to such an invitation becomes his or her activity. Ponte & Marques (2011) stresses that, the activity represents what the students actually do in terms of their thoughts and actions. According to the authors, tasks are external, whereas activities are internal to the student.

In general, according to Sullivan et al. (2013), tasks are seen as methods for launching activity” andthey create possibilities for mathematical learning.  As a result, according to Stein et al. (1996) textbooks tasks “may possibly impact and structure students’ thinking and can serve to limit or widen their view of the subject matter in which they are involved. As Gracin (2018) mentioned that it is critical that textbooks and other curricular materials used within classrooms give “rich” and valuable mathematical tasks.

Because textbook tasks and examples have a significant impact on mathematics instruction, it is acceptable to ask about the nature and demands of these tasks, if they serve to improve mathematical comprehension, and to what degree they are characterized as rich.

4. Methods:

According to Van Dormolen (1986), there are three types of textual analysis:

• A priori textual analysis: Analyzing a text as a possible means of instruction.
• A posteriori textual analysis: Comparing learning results with the text.
• Tempo textual analysis: Analyzing how teachers and learners use texts in the teaching-learning activities.

We will focus on the first type for the goals of this study as a first step of textbooks analysis.

This study is based on document analysis and employs a content analysis technique. We started by selecting the topic. We chose the concept of quadrilaterals in grade 8 since it is a fundamental element of the geometry curriculum. We selected the topic of parallelogram in grade 8, because, in the Lebanese curriculum, trapezoid is given only with the midpoint theorem.NTCM (2000) stressed that the parallelogram is one the basic topics in geometry which involves the concepts of rectangle, square, rhombus and parallelogram.

In this study, all studied items are referred to as tasks; the term “task” refers to any problem-situation in textbooks that require an answer, regardless of whether the solution is provided or not. The majority of them are exercises, although there are also worked examples, revision tasks, and other problems. All tasks in textbooks, except those used at the introduction, were coded. Only the learners; editions of textbooks were used.

The textbooks used in this study were the National Lebanese textbook along with two other textbooks with large market share thereby indicating a distinct trend in Mathematics instruction (Table 1). The English version of these book was selected since it’s the common language between the authors. For the purposes of the study the three textbooks will be referred to as textbook A, textbook B and textbook C as mentioned in the Table 1 below.

Table 1: Textbooks selected in this study

Title	Code	Publisher	Collection
Mathematics Intermediate Level – 8th year	A	Al Ahlia	Puissance
Math Grade 8	B	Hachette Antoine S.A.L	THEMA
Building up MATHEMATICS – 8th Grade. Basic Education.	C	Center for Education Research and Development (CERD)	National textbook

 

The chapters focusing on the concept of parallelograms were included in the analysis. We chose from Textbook A two chapters called: Parallelogram and Special Parallelogram. From Textbooks B we chose one chapter called: Parallelograms and Special Parallelograms. At last, we chose from textbook C four chapters called: The Square, The Rectangle, The Rhombus and The parallelogram.

The three textbooks (7 chapters altogether) were analyzed with an instrument that included two frameworks: One for global analysis and another one for task analysis.

The first framework used in Ponte & Marques (2008) and considers the physical appearance (Number of volumes, Paper size format, number of pages, significance of the cover), accessibility of language, nature and role of illustrations, number of chapters under the topic chosen and the internal organization of the chapters.

Because different types of mathematical tasks have diverse characteristics, their analysis is complicated. The goal of this study is to analyze the characteristics and diversity of textbooks tasks using a multidimensional framework. Therefore, the second framework which assess the requirements in textbook tasks, was adapted by Glacin (2018). The 5D framework comprises of the following elements: Content, Mathematical activities, complexity levels, answer forms, and contextual features. Glacin’s (2018) framework was employed because it was specifically created to analyze mathematics tasks in textbooks. The following five subsections contain descriptions of the five mentioned dimensions.

6.1 Content:

The content requirements apply to determining what mathematical knowledge a student should have in order to complete a specific textbook task. We distinguish here four content fields coded as follows: Numbers and measures (Coded C1); Variables and functional dependences (Coded C2); Geometric shapes and solids (Coded C3) and Statistics representations and parameters (Coded C4).

6.2- Mathematical activities:

The aim of this dimension is to find out what should be done in a particular task. The dimension of Mathematical activity is separated into the following categories: Representation and modeling, Computation and operation; Interpretation and Argumentation and reasoning.

The concept of representation (Coded A1) refers to the “Transformation” of given mathematical data into another mathematical representation. As for the modelling component (Also coded A1), it’s about recognizing significant mathematical relationships from a particular situation and describing the same problem in a mathematical style (Symbolic, graphical, etc.).

Calculation (Coded A2) is concerned with performing basic computation operations with concrete or generalized numbers. The concrete, sensible and efficient execution of computational or constructional procedures is known as operation (Also coded A2). It also refers to converting measure units, converting mathematical statement, calculating equations, estimating results, approximations, and performing rudimentary geometrical construction.

Interpretation (Coded A3) is concerned with understanding relationships and important data in mathematical representations (Graphical, symbolical, and tabular) and interpreting them in the given context. Interpreting entails reading relevant graphical or symbolical mathematical representations and interpreting them in the current context.

Argumentation (Coded A4) is the description of mathematical aspects that advocate for or against a specific decision. It necessitates the concrete and suitable use of mathematical relations and characteristics, mathematical principles, and the accurate application of mathematical language. The chain of true arguments that leads to a conclusion is referred to as reasoning (Also coded A4).

6.3- Complexity level:

The complexity dimension is separated into three categories: direct application of basic knowledge and abilities, connection construction and management, and reflection or application of reflective knowledge.

Applying fundamental knowledge and skills (Coded L1) entails reproducing or directly applying mathematical concepts, rules, procedures and representations. Making connections (Coded L2) and dealing with connections are more difficult tasks that need the combination of numerous concepts or activities in order to address the problem. Making connections between various concepts, theorems, procedures, and representations is one example. Reflective thinking (Coded L3) entails thinking about mathematical ideas that are not obvious from the provided problem. Reflective knowledge is the application of creative mathematical knowledge.

6.4- Answer form:

          The dimension of answer form contains the following categories: Open-ended tasks, Closed-ended tasks and Multiple-choice tasks. Open-ended tasks (Coded F1) contain multiple valid answers, whereas closed-ended tasks (Coded F2) have just one proper response. Multiple-choice response (Coded F3) that provide a “limited number of defined response-options.

6.5- Contextual features:

Contextual dimension refers to the extent and manner in which real-world experiences are integrated into textbook tasks.  A non-application task (R1) is unrelated to the real world, while an application problem (R2) arises in the context of a real-life situation.

The Table 2 below summarize the second framework used with the related codes.

Table 2: 5D framework for task analysis

Dimension	Question	Details and codes
Mathematical content	What information does a student need to know in order to complete a specific task?	Numbers and measures (C1) Variables and functional dependences (C2) Geometric shapes and solids (C3) Statistics representations and parameters (C4).
Mathematical activity	What mathematical activities need to be carried out in order to complete the task successfully	Representations and modelling (A1) Calculation and operation (A2) Interpretation (A3) Argumentation and reasoning (A4)
Complexity level	What is the level of complexity of knowledge and activities required for a student to complete the task?	Applying fundamental knowledge and skills (L1) Making connections (L2) Reflective thinking (L3)
Answer form	What the answer form does the task require?	Open-ended (F1) Closed-ended (F2) Multiple-choice (F3)
Context	What is the task context?	Non-application (R1) Application (R2)

Each textbook exercise (May contains many tasks) was analyzed to see which categories were required (content, activity, complexity level, answer form and context, as shown in Table 2).

Except for those used during the topic’s introduction, all tasks in the textbook’ learning exercises and worked-out examples were coded for this study. Before the coding begins, a meeting took place between the three coders (Authors): The first one is a university professor and former head of education department with a big experience in curriculum and textbooks, the second is a doctoral student in Mathematics education with an experience in teaching and curriculum development, and the third hold a master degree in Mathematics education with a big experience in teaching mathematics. Questions were coded and the coding was discussed throughout this meeting.

Later on, the three coders separately coded all of the questions, and the results were compared. In any category where the reliability was less than 90%, the questions that had been coded incorrectly were revisited and recoded. The reliability was calculated using the most recent coding. The reliability calculated for each category was found to be 94% for mathematical content, 98% for Mathematical activities, 96% for complexity level, 97% for answer form and 96% for contextual features.

As previously stated, the purpose of this study is to examine the tasks used to assist students in systematizing and consolidating their knowledge, and to discover similarities and differences among textbooks. To accomplish this purpose, we collected information on the following points: (1) How are the textbook regarding their physical features, language and illustrations? (2) What is the organization of the textbooks and the structure of the chapters? (3) How do the tasks pertaining the topic compare in the textbooks with respect to their mathematical content? (4) How do the tasks pertaining the topic compare in the textbooks with respect to their mathematical activities? (5) How do the tasks pertaining the topic compare in the textbooks with respect to their complexity level? (6) How do the tasks pertaining the topic compare in the textbooks with respect to their answer forms? (7) How do the tasks pertaining the topic compare in the textbooks with respect to their contextual features? (8) To what extent do the textbooks offer the full range of task types?

Example of a task analysis:

This section presents one task from textbook B (p. 64, Exercise n’6). It is then followed by an analysis based on the 5D framework chosen for this study.

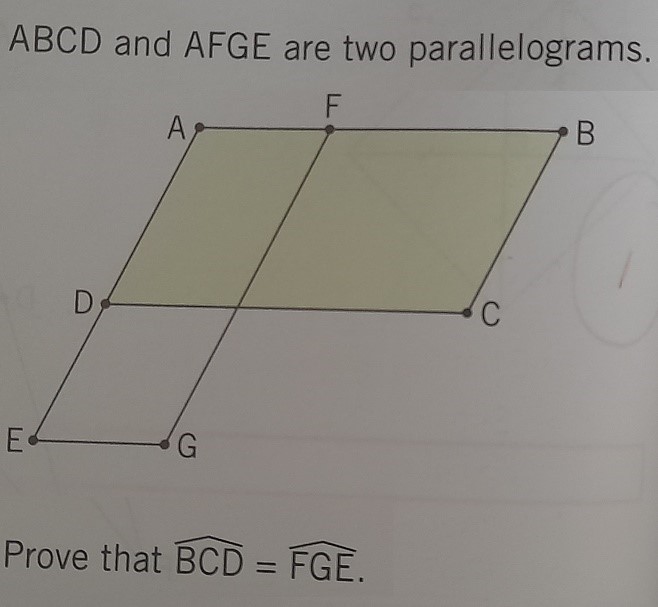
The exercise mentioned above contains only one task: Prove that . No construction of drawing is required from the student.

This task is on the Geometric shapes and solids content C3 (Table 2). This necessitates an argumentation and reasoning activity (A4) since the student have to write a proof to answer the question. The task is assigned the intermediate level of complexity (Making connections: L2). The task is purely mathematical context (Non-application: R1) and the needed answer is open (F1).

5. Results:

The findings are organized into six sections that correspond to the framework’s five dimensions along with a section dedicated to the general analysis.

Section 1: General aspects

          The first research question investigates the physical characteristics of the textbooks, as well as the language used and illustrations they give. The three textbooks are in one volume and have comparable paper size formats (A4). Textbooks B comes with a digital desktop version. Regarding the number of pages, all three textbooks have similar number of pages: 271 pages for Textbook A, 264 pages for Textbook B and 225 for Textbook C. The covers of Textbooks A and B are not directly linked to Mathematics, whereas the cover of Textbook C displays a strong relationship with the subject.

          All textbooks provide a language that students in grade 8 level in Lebanon can understand. Furthermore, all textbooks are widely illustrated by pictures, drawing and photographs. Outside the context of geometry, these illustrations do not represent any relevant information to solve the problem. In the context of geometry, textbooks mainly contain drawings related to the problem.

          The second research question investigates the organizations of the textbooks related to the topic chosen (Number of chapters) and the structure of the chapters. The topic of parallelogram is divided between two chapters in Textbook A (Namely: Parallelogram and Special Parallelogram), one chapter in textbook B (Namely: Parallelograms and Special Parallelograms) and four chapters in textbook C (Namely: Square, Rectangle, Rhombus and Parallelogram).

          There are, nevertheless, significant differences in the discourse of the three textbooks in terms of chapters structure. The chapters in Textbooks A and C are organized in a consistent style that varies little from one another. In various numbers and levels of complexity, both textbooks provide revision tasks, introductory tasks, application tasks and consolidation tasks. Textbook A follows a different pattern: It explains the concept directly, give a synthesis, and ultimately propose a battery of tasks for practice.

• Textbooks Tasks:

There were 346 tasks in the chapters directly related to the topic of parallelograms in Textbook C but fewer in Textbooks A and B (185 and 211 tasks respectively). Fewer questions may result in fewer diversity within tasks with respect to the dimensions mentioned in the chosen framework (Ozer &Sezer; 2014). We now address the way the tasks proposed in the textbooks vary in terms of Mathematical content, Mathematical activity, Complexity level, Answer form and Context as mentioned in Table 2.

Section 2: Content:

	Textbook A	Textbook B	Textbook C
Numbers and measures (C1)	4 (2.2%)	1 (0.5%)	18 (5.2%)
Variables and functional dependences (C2)	3 (1.6 %)	9 (4.2 %)	32 (9.2 %)
Geometric shapes and solids (C3)	178 (96.2 %)	201 (95.3%)	295 (85.3%)
Statistics representations and parameters (C4)	0 (0%)	0 (0%)	1 (0.3 %)

Table3: Content of tasks presented in textbooks (Number and percentage).

The third research question investigates and compare textbooks tasks with respect to their content. Geometric shapes and solids content tasks predominate in all textbooks studied – accounting for more than 85 % of the total number of tasks. Such tasks account for 96.2 % for Textbook A, 95.3 % for Textbook B, and 85.3% for textbook C. Other content tasks on the other hand, are underrepresented in most textbooks as shown in the table 3 above. This result might sound normal since we’re comparing the three textbooks based on one specific geometric topic, but mixing topics within the same task might be beneficial to the students (Glacin, 2018).Numbers and measures content have stronger presence in Textbook C (5.2%), followed by Textbook A (2.2%) ending by Textbook B (0.5%). Variables and functional dependences have stronger presence also in Textbook C (9.2%), followed this time by Textbook B (4.2%) ending by Textbook A (1.3%). Finally, Statistics representations and parameters are not present in Textbook A and B. In Textbook C it’s present in only one tasks making 0.3% from the total number of tasks. The distribution of these tasks based on their mathematical content is given in Table 3. As we may see in this dimension, Textbook C seems providing more diverse tasks from the other textbooks selected for this study.

Section 3: Mathematical activity:

	Textbook A	Textbook B	Textbook C
Representations and modelling (A1)	11 (5.9 %)	20 (9.5 %)	66 (19 %)
Calculation and operation (A2)	16 (8.7 %)	10 (4.7 %)	18 (5.2 %)
Interpretation (A3)	14 (7.6 %)	6 (2.9 %)	17 (4.9 %)
Argumentation and reasoning (A4)	144 (77.8 %)	175 (82.9 %)	245 (70.9 %)

Table 4: Mathematical activity of tasks presented in textbooks (Number and percentage).

The fourth research question investigates and compare textbooks tasks with respect to the mathematical activity required from the student.  When tasks were assessed based on the mathematical activities required, we notice a higherpercentage of Argumentation and reasoning tasks in the three textbooks. Such activities cover 77.8 % from Textbook A, 82.9 % from Textbook B and 70.9 % of Textbook C. Representations and modelling activity have stronger presence also in Textbook C (19%), followed by Textbook B (9.5%) ending by Textbook A (5.9%). As for Calculation and operation activity, the results show that it has stronger presence in Textbook A (8.7%), followed by Textbook C (4.9%) ending by Textbook B (4.7%). Finally, the interpretation activity, have stronger presence in Textbook A (7.6%), followed by Textbook C (4.9%) ending by Textbook B (2.9%). In this dimension also, we notice that Textbook C stands up with more diverse tasks. The distribution of these tasks based on their mathematical activities is given in Table 4.

 

Section 4: Complexity level:

	Textbook A	Textbook B	Textbook C
Applying fundamental knowledge and skills (L1)	11 (6 %)	8 (3.8 %)	6 (1.7 %)
Making connections (L2)	174 (94 %)	202 (95.7 %)	334 (96.6 %)
Reflective thinking (L3)	0 (0%)	1 (0.5 %)	6 (1.7 %)

Table 5: Complexity level of tasks presented in textbooks (Number and percentage)

.

The fifth research question investigates and compare textbooks tasks with respect to their complexity level. Due to the absence of complexity criteria in the Lebanese Mathematics program (1997), the level of complexity in textbook tasks is mostly determined by the authors. Of those tasks, we see predominance of connections tasks making 94 % in Textbook A, 95.7 % in Textbook B and 96.6 % of Textbook C. In contrast, application and reflection tasks are little represented in all textbooks. Application tasks have stronger presence in Textbook A (6%), followed by Textbooks B (3.8%), ending by Textbook C (1.7 %). Reflective tasks have stronger presence in Textbook C (1.7%), followed by Textbook B (0.5%) ending with Textbook A where no reflective thinking tasks were seen.In this dimension, all three textbooks don’t seem to provide a variety of tasks. The distribution of these tasks in the textbooks is given in Table 5.

Section 5: Structure:

	Textbook A	Textbook B	Textbook C
Open-ended (F1)	130(70.3 %)	153 (72.5 %)	204 (58.9 %)
Close-ended (F2)	38 (20.5 %)	45 (21.3 %)	131 (37.9 %)
Multiple-choice (F3)	17 (9.2 %)	13 (6.2 %)	11 (3.2%)

Table 6: Answer structure of tasks presented in textbooks (Number and percentage)

.

The sixth research question investigates and compares textbooks tasks with respect to the answer form or structure required from the student. In all textbooks analyzed, open-ended responses type is of the highest percentage making 70.3% of tasks in Textbook A, 72.5 % of tasks in Textbook B and 58.95 of Textbook C. In second place, textbooks present closed-ended responses tasks. Textbook C stands up by the large percent of this kind of tasks with 37.9% followed by Textbook B with 21.3%, closely followed by Textbook A with 20.5%. In contrast, multiple choice response tasks are little represented in all textbooks. They have stronger presence in Textbook A (9.2%), followed by textbook B (6.2%) ending with Textbook C (3.2%). As we may see in this section, Textbook C present more variety of tasks’ answer structure than the other books.The distribution of these questions in the textbooks is given in Table 6.

Section 5: Context

	Textbook A	Textbook B	Textbook C
Non-application (R1)	185	211	346
Application (R2)	0	0	0

Table 7: Contexts of tasks presented in textbooks (Number and percentage).

The seventh research question investigates and compares textbooks tasks with respect to their context. The results shown in the Table indicate the usage of non-application tasks to a huge extent (100% in all textbooks). Although mathematics has always been important in its application to real-world problems and recommended in the curriculum (1997): “It provides students with the skills they need for social interaction as well as effective tools for understanding and exploring the real world, regardless of the subject matter – physical, chemical, biological, astronomical, social, psychological, computer, etc.”, the results show that parallelogram topic is presented as a pure mathematical object.

6. Discussion:

          As we’ve seen, the textbooks under study have some common characteristics. Regarding the three textbooks’ physical attributes, they are all included in a single volume and have similar page size format. The number of pages of the three textbooks are comparable. Textbooks A and B have covers unrelated to mathematics, but textbook C have a cover that is specifically related to the subject.

          Every textbook uses a language and a terminology that eighth-grade students in Lebanon can understand. In addition, every textbook has a substantial number of images, drawings and photographs. These illustrations don’t provide any information that may be used to solve the problem outside the context of geometry. In chapters related to geometry, all textbooks typically provide drawings that is used to solve the problem.

          Overall research findings indicate that there is no equilibrium between various tasks types. The textbooks tasks are found to be mainly related directly to Geometric shapes and solids (Content), using argumentation and reasoning (Activity), in the level of making connections (Complexity), using open ended response (Structure) and intra-mathematics (Context). As we have seen in the results, Textbook C (The national mathematics textbook) has more diverse tasks than the other two books.

          The findings draw attention to the challenges in task design, particularly for tasks found in textbooks, which are frequently used as curriculum resources. Because textbook requirements affect implemented curriculum and students’ learning chances, task design difficulties are currently acknowledged as an intriguing and significant field with the research on mathematics education (Sullivan et al., 2013). Better implementation of a variety of tasks types(Sullivan et al., 2013 ;Stenmark, 1991) would promote the use of tasks that foster different types of content, different activities, using different structure, different complexity level and in different context with focus on real-life exercises and tasks. Because textbooks tasks assist students in creating possibilities that might either widen or restrict their perspectives on mathematics, this may have an impact on how the students perceive mathematics (Sullivan et al., 2013; Henningsen &Stein, 1997). A potential research topic is the relationship between the characteristics of textbook tasks, the actual mathematical curriculum, and students’ perception of mathematics.

7. Conclusion and recommendation:

          This article demonstrates how an analytical framework based on notions of didactics may be used while studying mathematics textbooks. In this work, the emphasis was on the suggested tasks in 3 selected textbooks in Lebanon. The results show the dominance of specific tasks types over other types.

          On one hand,this study suggests expanding both the number and variety of tasks. Labeling tasks in terms of each dimension in the used framework would be beneficial. Textbooks authors in Lebanon could benefit from such labeling to help teachers become more aware of the kind of tasks they are posing. Most of the tasks found have the potential to be easily modified to create rich tasks.

On the other hand, when evaluating textbooks for adoption as well as when planning their lessons and deciding what to advise students to do, the teachers must take a number of factors into account. The most important question that should be asked based of this article: Is there a range of tasks in the textbook in terms of content, activity, complexity level, answer form and context?

We find it intriguing to see how various textbook types are used in practice by students and teachers for upcoming studies. It would be particularly interesting to see how much the learning opportunities offered by those textbooks are implemented in classroom activities and, most importantly, in student learning. Finally, this study can be conducted again using different framework such as PISA or TIMSS.

References

• Abdullah, A., & Shin, B. (2019). A comparative study of quadrilaterals topic content in mathematics textbooks between Malaysia and South Korea. Journal onMathematics Education, 10, 315–340. https://doi.org/10.22342/jme.10.3.7572.315-340
• Christiansen, B., & Walther, G. (1986). Task and Activity (B. Christiansen, A. G. Howson, & M. Otte, Eds.; pp. 243–307). Springer Netherlands. https://doi.org/10.1007/978-94-009-4504-3_7
• Fan, L., Mailizar, M., Alafaleq, M., & Wang, Y. (2018). A Comparative Study on the Presentation of Geometric Proof in Secondary Mathematics Textbooks in China, Indonesia, and Saudi Arabia (pp. 53–65). https://doi.org/10.1007/978-3-319-73253-4_3
• Gracin, D. (2018). Requirements in mathematics textbooks: A five-dimensional analysis of textbook exercises and examples. International Journal of Mathematical Education in Science and Technology, 49, 1–22. https://doi.org/10.1080/0020739X.2018.1431849
• Henningsen, M., & Stein, M. K. (1997). Mathematical Tasks and Student Cognition: Classroom-Based Factors That Support and Inhibit High-Level Mathematical Thinking and Reasoning. Journal for Research in Mathematics Education, 28(5), 524–549. https://doi.org/10.2307/749690
• Hidayah, M., &Forgasz, H. (2020). A comparison of mathematical tasks types used in Indonesian and Australian textbooks based on geometry contents. Journal onMathematics Education, 11(3), 385–404. https://doi.org/10.22342/JME.11.3.11754.385-404
• Hong, D. S., & Choi, K. M. (2018). Reasoning and Proving Opportunities in Textbooks: A Comparative Analysis. International Journal of Research in Education and Science, 4(1), 82–97.
• Howson, A. G. (1995). Mathematics Textbooks: A Comparative Study of Grade 8 Texts. Pacific EducationalPress.
• Johansson, M. (2007). Mathematical Meaning Making and Textbook Tasks. For the Learning of Mathematics, 27(1), 45–51.
• Mithans, M., &Grmek, M. (2020). The Use of Textbooks in the Teaching-Learning Process (pp. 201–228). https://doi.org/10.18690/978-961-286-358-6.10
• NCTM (2000). Principles and standards for school mathematics. Reston, VA: NCTM.
• Otten, S., Males, L. M., & Gilbertson, N. J. (2014). The introduction of proof in secondary geometry textbooks. International Journal of Educational Research, 64, 107–118. https://doi.org/10.1016/j.ijer.2013.08.006
• Ozer, E., &Sezer, R. (2014). A Comparative Analysis of Questions in American, Singaporean, and Turkish Mathematics Textbooks Based on the Topics Covered in 8th Grade in Turkey. EducationalSciences: Theory and Practice, 14(1), 411–421.
• Ponte, J., & Marques, S. (2011). Proportion in school mathematics textbooks: A comparative study. International Journal of Research. https://www.semanticscholar.org/paper/Proportion-in-school-mathematics-textbooks%3A-A-study-Ponte-Marques/c0ccd72d7132c0aadfdde9f7215ffff7883cf180
• Remillard, J. T. (2000). Can curriculum materials support teachers’ learning? Two fourth-grade teachers’ use of a new mathematics text. The Elementary School Journal, 100, 331–350. https://doi.org/10.1086/499645
• Rezat, S. (2013). The textbook-in-use: Students’ utilization schemes of mathematics textbooks related to self-regulated practicing. ZDM, 45, 659–670. https://doi.org/10.1007/s11858-013-0529-z
• Skovsmose, O. (2001). Landscapes of Investigation. ZentralblattFürDidaktik Der Mathematik, 33(4), 123–132. https://doi.org/10.1007/BF02652747
• Stein, M. K., Grover, B. W., & Henningsen, M. (1996). Building Student Capacity for Mathematical Thinking and Reasoning: An Analysis of Mathematical Tasks Used in Reform Classrooms. American EducationalResearch Journal, 33(2), 455–488. https://doi.org/10.3102/00028312033002455
• Stenmark, J. K. (1991). Mathematics Assessment: Myths, Models, Good Questions, and Practical Suggestions. National Council of Teachers of Mathematics, 1906 Association Drive, Reston, VA 22091-1593 ($8.
• Sullivan, P., Clarke, D., & Clarke, B. (2013). Teaching with Tasks for Effective Mathematics Learning. https://doi.org/10.1007/978-1-4614-4681-1
• Usiskin, Z. (2013). Studying textbooks in an information age—A United States perspective. ZDM, 45. https://doi.org/10.1007/s11858-013-0514-6
• Usiskin, Z., Griffin, J., Witonsky, D., & Willmore, E. (2008). The classification of quadrilaterals: A study of definition. https://www.semanticscholar.org/paper/The-classification-of-quadrilaterals-%3A-a-study-of-Usiskin-Griffin/c258137b594731c413f8f6f3e5bb929cd8f6d4fa
• Valverde, G. A., Bianchi, L. J., Wolfe, R. G., Schmidt, W. H., &Houang, R. T. (2002). According to the Book. Springer Netherlands. https://doi.org/10.1007/978-94-007-0844-0
• Van Dormolen, J. (1986). Textual Analysis. In B. Christiansen, A. G. Howson, & M. Otte (Eds.), Perspectives on Mathematics Education: Papers Submitted by Members of the Bacomet Group (pp. 141–171). Springer Netherlands. https://doi.org/10.1007/978-94-009-4504-3_4
• Xin, Y. P. (2007). Word problem solving task in textbooks and their relation to student performance. The Journal of EducationalResearch, 100, 347–359. https://doi.org/10.3200/JOER.100.6.347-360

[1] – PHD Student, University Saint Joseph (USJ), Beirut, Lebanon- Eliekhoury14@hotmail.com

[2] – Masters in Maths didactics,   Lebanese university, Beirut, Lebanon- Rosesfeir@gmail.com

[3] – USJ  University  and  University Of Balamand    (AOB) , Koura,  Lebanon – Naim.rouadi@gmail.com